LeetCode53-MaximumSubarray(最大子序和)

LeetCode:https://leetcode-cn.com/problems/maximum-subarray/

LeetCodeCn:https://leetcode-cn.com/problems/maximum-subarray/

题目描述

给定一个整数数组 nums ，找到一个具有最大和的连续子数组（子数组最少包含一个元素），返回其最大和。

示例:

输入: [-2,1,-3,4,-1,2,1,-5,4],
输出: 6
解释: 连续子数组 [4,-1,2,1] 的和最大，为 6。

解题思路-分治

此条件下,我们可以发现连续子数组的序列和最大的时候其首位不能为负数,原因很简单,如果首位为负数,当拿掉首位时,其剩余的数组和必然会增大.同理可扩展,如果某几项的和为负数时,则这几个数也不能作为和最大的子数组的开始

当了解了以上的内容时,我们可以采用分治的方法来解决此问题.
我们已一个非负数为开始,直到和为负数为结束,再此过程中比较其和的最大值并记录,重复以上过程直到遍历到数组结束.

图解相关思路

下面已[-2,1,-3,4,-1,2,1,-5,4]为例,我们需要通过i遍历一次nums的内容,额外使用sum用来记录当前子数组的和(默认为0),result为遍历过程中遇到的最大和(默认为nums[0])

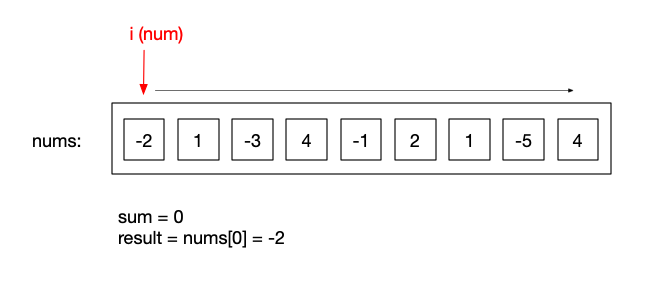
当i=0时,sum不大于0,我们要已此位(i=0)为子数组的开始,同时例行检查result和sum的关系

i=0

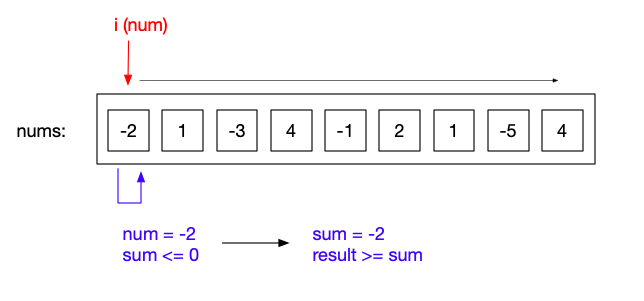
当i=1时,此时sum=-2,要小于0,此时和为-2的子数组[-2]不能为最大子数组的开始,将sum更新为num=1,result更新为1

i=1

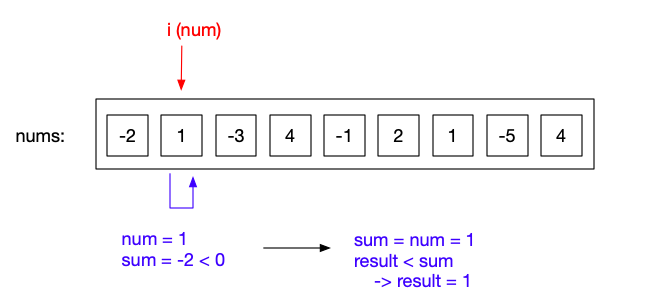
当i=2时,此时sum=1,要大于0,sum要+=num为-2

i=2

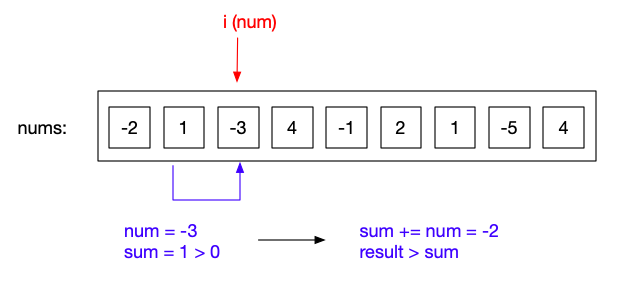
当i=3是,此时sum为-2,我们需要将此为作为新的子序列的开始,相关变化如下图

i=3

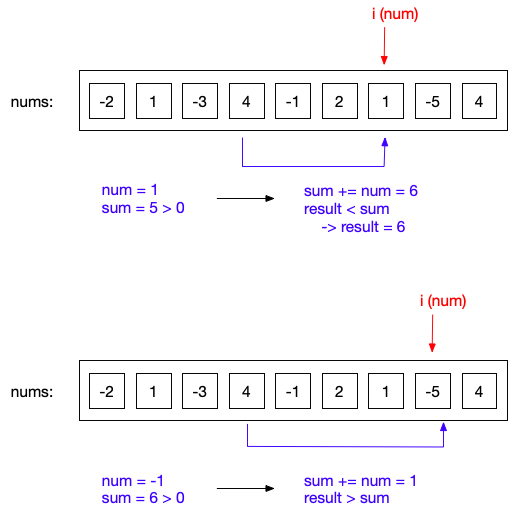
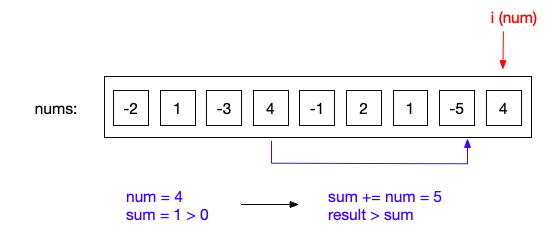
当i=4,5,6,7,8时,sum均大于0,检测result和sum值即可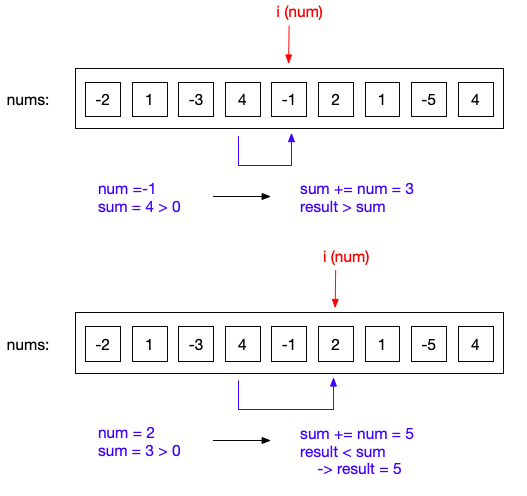
i=4,5

i=6,7

i=8

代码实现

public int maxSubArray(int[] nums) {
    int result = nums[0];
    int sum = 0;
    for (int i = 0 ; i < nums.length ; i++){
        if (sum > 0){
            sum += nums[i];
        }else {
            sum = nums[i];
        }
        if (sum > result){
            result = sum;

        }
    }

    return result;
}