Leetcode70-ClimbingStairs(爬楼梯)
LeetCode:https://leetcode-cn.com/climbing-stairs/
LeetCodeCn:https://leetcode-cn.com/climbing-stairs/
题目描述
假设你正在爬楼梯。需要 n 阶你才能到达楼顶。
每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢?
注意:给定 n 是一个正整数。
示例
示例 1:
- 输入: 2
- 输出: 2
- 解释: 有两种方法可以爬到楼顶。
- 1 阶 + 1 阶
- 2 阶
示例 2:
- 输入: 3
- 输出: 3
- 解释: 有三种方法可以爬到楼顶。
- 1 阶 + 1 阶 + 1 阶
- 1 阶 + 2 阶
- 2 阶 + 1 阶
解题思路-迭代法
一道很经典的题,这个题可以转化为求斐波那契数列数列第n项的问题.可以才用递归的方法,不过在递归的过程中有大量的重复计算导致其性能一般(可以通过设置计算缓存来避免).
初次之外,还可以用迭代的方法来降低消耗的资源.
原理很简单,应为斐波那契数列从第三项起,其值为前两项的和,我们可以通过不断的计算前两项和,并更新前两项的数据来获得最新项的值
图解相关思路
下面我们给出斐波那契数列数列的前十项,并令a为第一项(0),b为第二项(1)
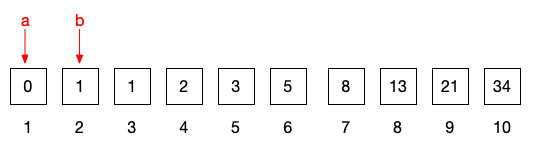
当我们求第三项的时候,我们先创建一个临时变量用于储存a,将a指向b,将b指向下一位(应计算的位置),并将原来的b值和变化前的a值(temp).简单来说就是将a和b都向后移动了一位

计算第四项及以后各项均类似,通过更改自身的值,并不断的去计算新的内容

代码实现
1 | public int climbStairs(int n) { |
相关代码欢迎大家关注并提出改进的建议